Θεώρημα 15. Έστω η συνάρτηση ![]() . Να αποδείξετε ότι η συνάρτηση
. Να αποδείξετε ότι η συνάρτηση ![]() είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο ![]() και ισχύει
και ισχύει ![]() δηλαδή
δηλαδή
![]()
(ΗΜ. 2008)
Έστω η συνάρτηση ![]()
- Αν
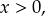 τότε
τότε 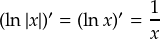
- Αν
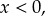 τότε
τότε 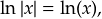 οπότε, αν θέσουμε \begin{center}
οπότε, αν θέσουμε \begin{center}
![]() και
και ![]() \end{center}
\end{center}
έχουμε y = lnu. Επομένως,
![]()
Άρα,
![]()