Θεώρημα 18. (Θ. Fermat) Έστω μια συνάρτηση 
ορισμένη σ’ ένα διάστημα Δ και 
ένα εσωτερικό σημείο του Δ. Αν η παρουσιάζει τοπικό ακρότατο στο 
και είναι παραγωγίσιμη στο σημείο αυτό, τότε να αποδείξετε ότι:
![\[\textcolor{blue}{ f '(x_0) = 0}\]](https://gbelentzas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-036f5974e867894dd452e1cd07ff80d4_l3.png "Rendered by QuickLaTeX.com")
(ΗΜ. 2004, ΗΜ. 2011)
Έστω μια συνάρτηση 
ορισμένη σ’ ένα διάστημα Δ και 
ένα εσωτερικό σημείο του Δ.
Ας υποθέσουμε ότι η f παρουσιάζει στο τοπικό μέγιστο.
Επειδή το είναι εσωτερικό σημείο του Δ και η παρουσιάζει σ’ αυτό τοπικό μέγιστο, υπάρχει 
τέτοιο, ώστε
και 
για κάθε 
Επειδή, επιπλέον, η είναι παραγωγίσιμη στο 
ισχύει
![\[f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}^{-}} \dfrac{f(x)-f\left(x_{0}\right)}{x-x_{0}}=\lim _{x \rightarrow x_{0}^{+}} \dfrac{f(x)-f\left(x_{0}\right)}{x-x_{0}}\]](https://gbelentzas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-e6d815545d87fc7c4ee0659abc9fcb4f_l3.png "Rendered by QuickLaTeX.com")
Επομένως,
- αν
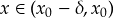τότε, λόγω της (1), θα είναι 
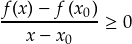οπότε θα έχουμε
![\[ f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}^{-}} \dfrac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \geq 0 \quad (2)\]](https://gbelentzas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-2267c34fef41a1b8a6ce61847a622bff_l3.png "Rendered by QuickLaTeX.com")
- αν
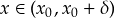τότε, λόγω της (1) , θα είναι 
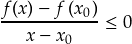οπότε θα έχουμε
![\[f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}^{+}} \dfrac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \leq 0 \quad (3)\]](https://gbelentzas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-04f693e168de4a0f3418e48f30af19e1_l3.png "Rendered by QuickLaTeX.com")
Έτσι, από τις σχέσεις (2) και (3) έχουμε 
Η απόδειξη για τοπικό ελάχιστο είναι ανάλογη.